티스토리 뷰

이진탐색트리 (Binary Search Tree)란, 기존의 이진 트리가 변형된 형태이다 . 이는 말 그대로 '탐색'을 더 효율적으로 하기 위해 설계된 자료구조로, 맨 위 노드를 기준으로 왼쪽은 맨 위 노드보다 작은 데이터가, 오른 쪽은 맨 위 노드보다 큰 데이터가 삽입된다. 또한, 모든 subtree는 이진탐색트리이므로, 모든 subtree에도 이러한 법칙이 적용된다.
그러면 이진탐색트리의 cpp 코드를 하나씩 살펴보도록 하겠다.
1. 트리 노드 타입
class BSTNode {
public:
int key;
BSTNode* left =NULL;
BSTNode* right = NULL;
};
2. BST 클래스
class BST {
public:
BSTNode* root = NULL;
void insert(int key) {}
bool remove(int key) {}
bool search(int key) {}
void preorder(BSTNode*root) {}
int find_min() {}
int find_max() {}
};해당 클래스는 BST의 ADT 를 담고있다. 보다싶이, ' BSTNode* root ' 를 public 멤버변수로 선언해줌으로써, 트리의 root를 생성했다. 이는 무조건 명시적으로 NULL로 초기화해주어야 한다. 그러지 않으면 접근 에러가 난다. 그렇다고 root에 동적할당을 해서도 안된다. 그러면 root는 원래 기능 (노드를 가리키는)을 잃고, 그 자체로 하나의 노드가 된다.
root는 앞으로 트리에서 맨 처음 올 노드를 가리키는데 사용될 것이다.
앞으로 클래스 내에 선언된 멤버함수들을 하나하나씩 살펴보겠다.
3. 삽입
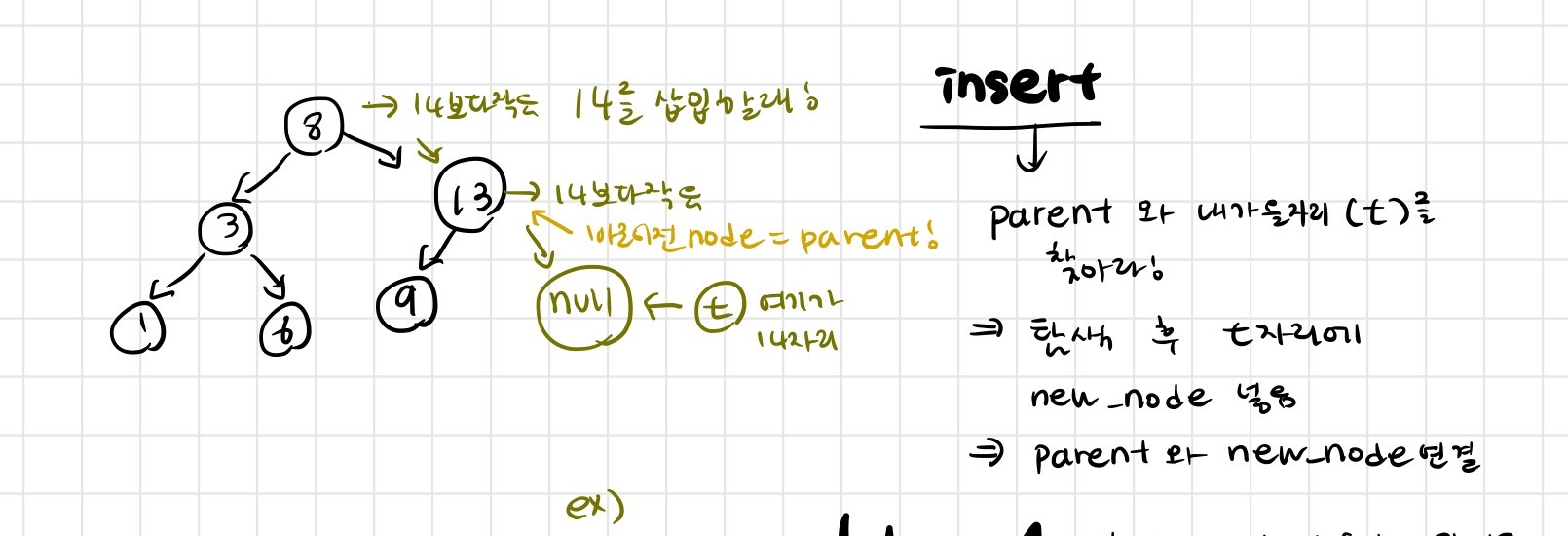
삽입은 삭제보다 간단한다. 일단 새로운 노드를 삽입하기위해서는 들어갈 알맞은 빈 자리와, 그 자리의 parent, 즉 부모노드의 정보가 필요하다. 부모노드의 정보로 완성된 트리와 새로운 노드를 연결 시킬 수 있기 때문이다.
이를 위해서는 root부터 내려오면서 탐색을 해주면 된다. 그리고나서, 만약 parent 노드가 null이라면 첫번째 노드이기 때문에, root 를 새로운 노드로 수정해준다.
void BST::insert(int key) {
// 매개변수로 받은 key로 새로운 node 생성
BSTNode* new_node = new BSTNode();
new_node->key = key;
new_node->left = new_node->right = NULL;
BSTNode* tmp = root; //탐색할 노드
BSTNode* parent = tmp; //부모가 될 노드
while (tmp != NULL) { //삽입될 자리에서 끝
parent = tmp;
if (tmp->key > key) tmp = tmp->left;
else if (tmp->key == key) return; //이미존재
else tmp = tmp->right;
}
if (parent == NULL) { //부모가 null이라면, 첫번째 노드
root = new_node;
}
else {
if (parent->key > key) { //부모보다 작다면 부모의 왼쪽에
parent->left = new_node;
}
else parent->right = new_node; //부모보다 크다면 부모의 오른쪽에
}
}
4.삭제
삭제는 BST에서 가장 까다롭다. 일단 삭제는 세가지의 경우로 나뉜다 .
첫번째, 삭제할 노드가 단말노드인 경우
두번째, 삭제할 노드의 자식이 하나인 경우
세번째, 삭제할 노드의 자식이 두개인 경우

첫번째는 그냥 삭제할 노드의 부모 -자식의 연결을 null 로 바꾸어주고, 해당 노드를 동적할당해제해주면 된다.
두번째 역시 삭제할 노드의 자식노드를 삭제할 노드의 부모와 연결시켜주고, 삭제할 노드는 동적할당해제 해주면 된다.
세번째가 약간 까다롭다. 세번째는 '후계자'를 찾아야하는데, 이 후계자는 삭제할 노드와 '가장 값이 가까워야'한다.
이는 두가지 선택지가 있다. 삭제할 노드의 왼쪽 자식에서 가장 큰 노드 or 삭제할 노드의 오른쪽 자식에서 가장 작은 노드.
여기서는 후자의 경우를 선택하겠다. (아무거나 써도 상관X 본인이 구현하기 편한걸 하면된다.)
물론 후계자를 삭제되는 노드의 자리에 옮겨준 후, 후계자에게 있을지도 모르는 자식노드는, 후계자 노드의 부모노드와 꼭 연결시켜주어야 한다.
bool BST::remove(int key) {
BSTNode* p, * child, * succ, * succ_p, * t;
//부모 //자식 //후계자 //후계자부모 //현재
p = NULL;
t = root;
while (t != NULL && t->key != key) { //탐색 , 삭제할 노드와 삭제할노드의 부모 탐색
p = t;
t = (key < p->key) ? p->left : p->right;
}
if (t == NULL) { //t가 null이면 못찾음
cout << " key is not in the tree" << endl;
return false;
}
if (t->left == NULL && t->right == NULL) { //단말노드
if (p != NULL) {
if (p->left == t) p->left = NULL;
else p->right = NULL;
}
else { //부모노드가 null -> 부모노드 없음 -> 삭제되는 노드는 root
root = NULL;
}
}
else if ((t->left == NULL) || (t->right == NULL)) { //자식하나
child = (t->left == NULL) ? t->right : t->left;
if (p != NULL) { //자식 - 조상 연결
if (p->left == t) p->left = child;
else p->right = child;
}
else {
root = child; //t가 root였던경우 root를 자식으로 바꿔줌
}
}
else { //자식 둘
succ_p = t; //후계자부모
succ = t->right; //후계자
while (succ->left!=NULL) {
succ_p = succ;
succ = succ->left; }
if (succ_p->left == succ) {
succ_p->left = succ->right; //만약 succ의 right 자식이 있다면
//부모에 연결
}
else { //succ_p->right==succ인 경우는 while문 실행하지 않은 경우
succ_p->right = succ->right;
}
t->key = succ->key; //후계자 값을 그냥t에 저장
t = succ;
}
delete t;
return true;
}
4. 탐색
특정 key값을 탐색하는 연산이다. 매우 쉽다. 계속 키값들을 비교해나가다가 값이 같은 노드를 찾는 것이다. 값을 찾지 못하면 false를 반환한다.
bool BST::search(int key) {
if (root == NULL) return false;
if (root->key == key) return true;
BSTNode* tmp = root;
while (tmp) {
if (tmp->key > key) tmp = tmp->left;
else if (tmp->key == key) return true;
else tmp = tmp->right;
}
return false;
}
5. 중위순회
중위순회는 left -> root -> right 순으로 출력한다. 다른 순회를 써도상관없다. binary tree를 이용해서 값을 정렬하고자 한다면 중위순회를 써야한다. 중위순회는 재귀함수이기 때문에 멤버함수임에도 불구하고 같은 멤버변수인 root를 따로 매개변수로 받아야한다.
void BST::inorder(BSTNode* root) {
if (root) {
inorder(root->left);
cout << root->key << endl;
inorder(root->right);
}
}
int main(void){
BST bst;
//생략
bst.inorder(bst.root);
}이런식으로 해주면된다.
6. 최솟값 최댓값
int BST::find_min() {
if (root == NULL) return -1;
BSTNode* tmp = root;
while (tmp->left!=NULL) { tmp = tmp->left; }
return tmp->key;
}
int BST::find_max() {
if (root == NULL) return -1;
BSTNode* tmp = root;
while (tmp->right != NULL) { tmp = tmp->right; }
return tmp->key;
}최솟값은 left를 타고 계속 왼쪽으로 내려가면 되고, 최댓값은 반대로 right을 타고 계속 오른쪽으로 내려가면 된다.
'algorithm > 자료구조 복습' 카테고리의 다른 글
| [자료구조 복습 8] 기초 정렬 알고리즘 정리 ( 선택, 삽입, 버블, 쉘) (0) | 2020.03.31 |
|---|---|
| [자료구조 복습7] 우선순위 큐 - Heap 구현하기 / Heap Sort (0) | 2020.03.30 |
| [자료구조 복습5] 이중연결리스트로 덱(double- ended queue) 구현하기 (0) | 2020.03.20 |
| [자료구조 복습4] 원형 큐와 연결리스트 큐 구현하기 (0) | 2020.03.18 |
| [자료구조 복습3] 연결리스트로 stack 구현하기 (0) | 2020.03.18 |
